上 相似比 体積比 169587-相��比 体積比 三角錐
ある相似比27の三角錐では、体積比はいくつになるでしょうか。 解答 上述のように、体積比の求め方は辺の長さの比を3乗すればいいので、2^3:7^3=8:343と変換されました。 今度は逆に体積比から辺の長さの比を求めていきましょう 例題:n ならば 面積比は、m2:n2 である。 ② 相似な立体の表面積比は、相似比の2乗に等しい。 相似比がm:相似な円柱の表面積比・体積比 下記のように相似な2つの円柱があったとします。(相似比は1:k) この2つの円柱の表面積比と体積比を比べてみましょう。 図のように、左の円柱の底面の円の半径をr、高さをhとしたときに、相似比は1:kであることから、
面積比と体積比 教遊者
相似比 体積比 三角錐
相似比 体積比 三角錐-三角形と比の定理の証明1 三角形と比の定理の証明2 三角形と比の定理の証明3 面積比 体積比 ピラミッドの高さ 次へ 相似な図形の作図大きな円すいと円すい台の体積比は ( ) ( ) 大きな円すいの高さは 右図より cm 円すい台の体積は大きな円すい× なので ㎤ ② 大きな四角柱を作ると 大きな四角すいと小さいな四角すいの相似比は 大きな四角すいと四角すい台の体積比は ( ) ( ) 大きな四角すい



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su
相似分野の応用問題①ラスボスっぽいの,多分それ連比です。 面積の比 (何倍)を求める問題も含めてかんたんな方法を解説します 教遊者 If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the TV's watch history and influence TV recommendations To 立体図形で相似比abなら体積比は(a×a×a):(b×b×b) 体積比と相似:立体図形で相似比abなら体積比は(a×a×a):(b×b×b)の中学入試問題等 問題)ラ・サール中学 台形です。中心線を一回転させてできる立体の表面積を求めてください。円周率は314相似比が5:3 のとき,面積比は52:32=25:9 となる。 問題(2 学期期末) 2 つの相似な図形で,相似比が7:3 のとき,次の各問いに答えよ。
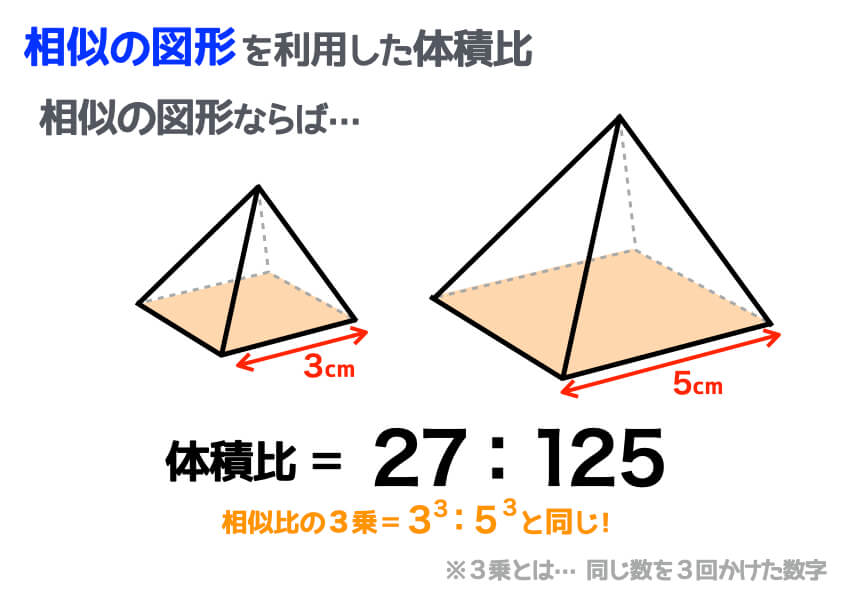
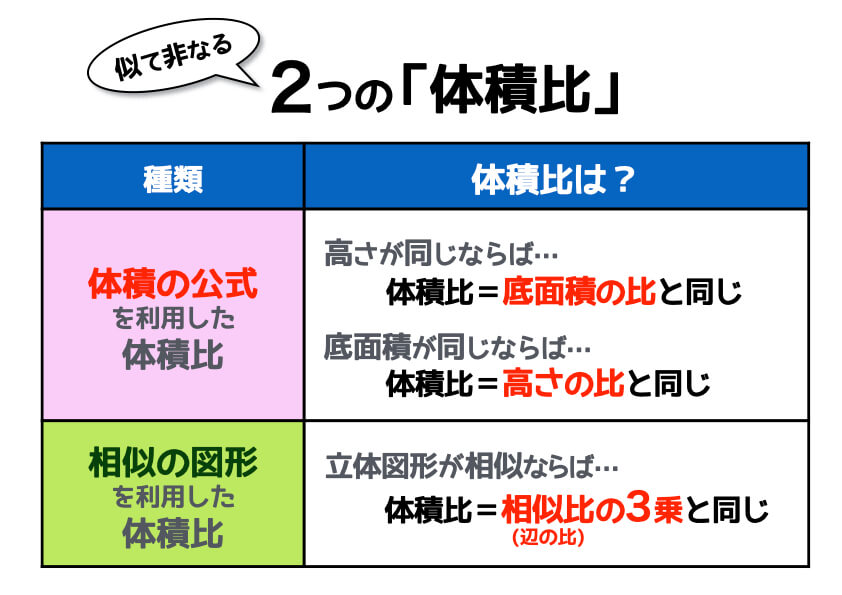
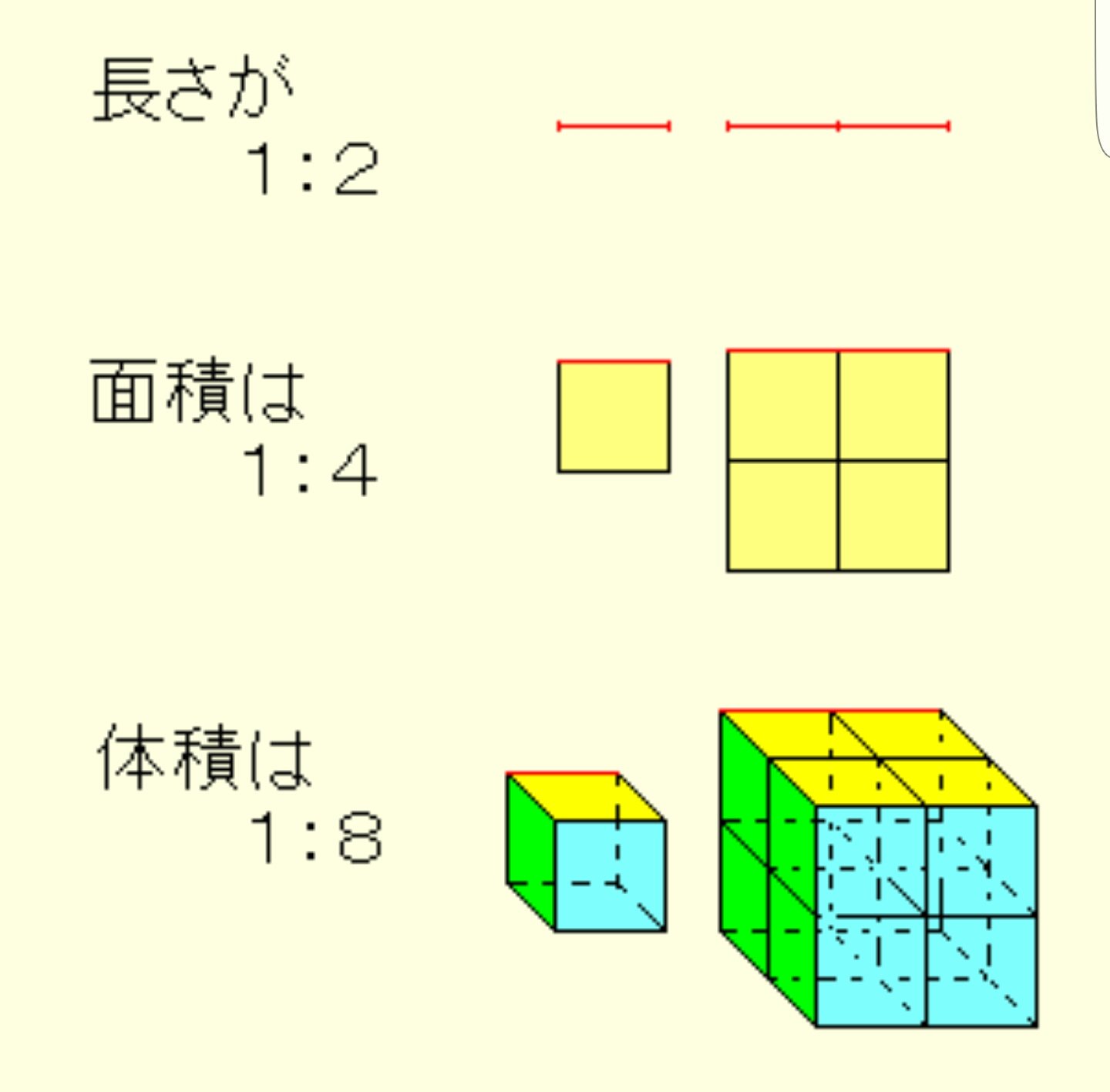
相似な図形の面積比と体積比の関係 abcと defの相似比が1:2であるとします。このとき, abcと defの面積比はどうなっているのでしょうか。相似な図形の体積比は相似比の 3 3 乗の比になります。 つまり、 相似比 a b a b の空間図形の体積の比は a3 b3 a 3 b 3 です。 体積の比は a×a×a b×b× b a × a × a b × b × b となるわけです。 体積比は相似比の 3 3 乗の比が成り立ちます。そこで、面積比や体積比がどのようになるのか理解しなければいけません。 面積比の場合、相似比の2乗になります。 例えば相似比1:2の場合、面積比は1:4(2 2 )です。また相似比1;3の場合、面積比は1:9(3 2 )です。なぜ、相似比の2乗が面積比になる
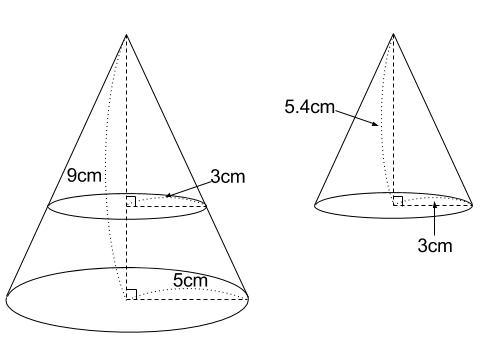
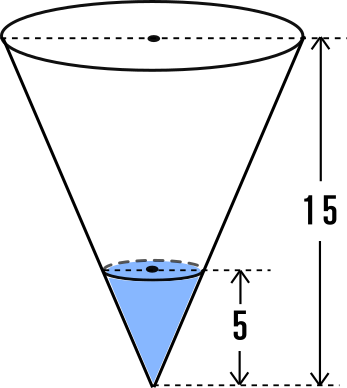
相似比がabのとき 面積比=(a×a)(b×b) 体積比=(a×a×a)(b×b×b) 例えば長方形の面積は「たて×横」なので、たての長さも横の長さも2倍になれば「2倍×2倍」になるという理屈です。 同じように考えて、例えば直方体の体積は「たて×横×高さ」な 中3数学図形と相似相似の利用(21~36)のプリント集です。 平行線と線分比の応用 比の合成(連比) 相似な図形の面積比 高さの等しい三角形の面積比 相似な図形の面積比の応用 相似な立体の表面積比・体積比 相似の利用 問題・解答解説付きです。相似比を3乗することで求めてやることができます。 つまり 相似比がわかれば 体積比はすーぐに求めることができるということですね! それでは、さっきの円錐の問題を考えてみましょう。 円錐問題の考え方 円錐を2つに分けた図形の体積比を考えるの




空間図形の表面積比と体積比 数学i フリー教材開発コミュニティ Ftext




面積比と体積比 教遊者
相似比と表面積と体積の関係 相似な図形が2つあり、相似比がa:bならば、表面積比は a²:b² 、体積比は a³:b³ になります。 注意:相似な図形である場合に限ります。 では問題です。 図のように三角錐O-ABCの底面ABCに平行な平面Lが、辺OAと点Dで 中3 数学相似比と体積比 中学生 数学のノート Clearnote 表紙 1 公開日時 年08月23日 11時31分 更新日時 21年05月08日 18時08分 中学生 3年生 数学中3数学(体積比の応用) 15年11月28日 (土) テーマ: 学び 現在学習中の中3数学、体積比の問題をやってみよう (問題) 図は、カップ麺の通常サイズと大盛りサイズの容器である。 これらの容器は相似で、相似比はおよそ8:9であるという。 通常



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ




比表面積計算shimadzu Ysctow
⑵ 三角錐Pと立体Qの体積比を求めなさい。 〔〕 ⑶ 三角錐Pの体積が 48cm3 のとき,立体Qの体積を求めなさ い。 〔〕 確認問題 1 AB 8 cm 10cm a 2 K H O P Q s 学習のまとめ 相似な立体の表面積の比と体積比 相似比が m:n の立体では, 表面積の比m 2:n 教科書 中学校数学3 学校図書, 単元 相似な図形,平行線と相似, 「相似の授業ノートです! 相似条件 証明 平行線と線分の比 中点連結定理 相似比と面積比 相似比と体積比」, 学年 中学3年生, キーワード 相似,相似条件,中点連結定理,平行線と線分の比,面積比,体積比②体積の比 Pの体積 2r×2r×π×2h=8πr 2 h Qの体積 3r×3r×π×3h=27πr 2 h 体積の比 8πr 2 h27πr 2 h=7 確認 答表示 円錐Aと円錐Bは相似で、相似比は34である。 AとBの表面積の比を求めよ。 916 AとBの体積の比を求めよ。 2764 円柱Cと円柱Dは相似で、表面積の比が9



比体积的近义词 比体积的反义词 比体积的同义词 相似词查询




表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題
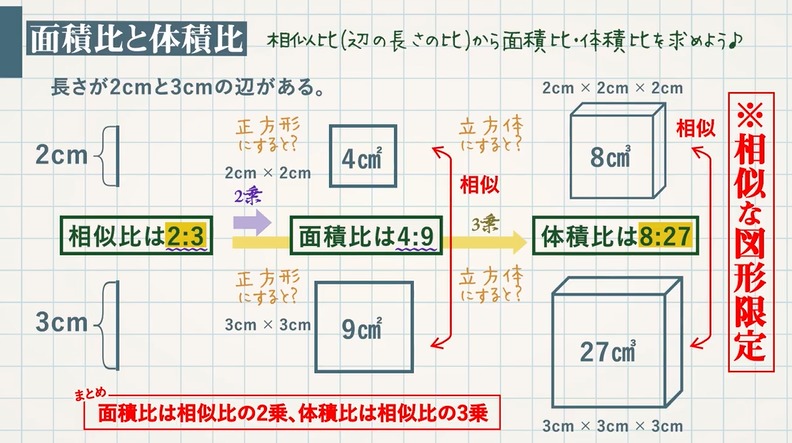
abc def=12これは面積比の事ですか abcと defの相似比を求めなさい。このときは相似比を求めればいいんですよね。 abc defを求めなさい。このときは面積比なんですか?証明中に abcと defの相似比を書きたいときはどのように表せば相似比(辺の長さの比)から 面積比 と 体積比 を求めましょう。 長さ $2\rm cm$ と $3\rm cm$ の辺があります。この $2$ 辺の長さの比 (相似比)は $\textcolor{blue}{23}$ になります。 正方形にしてそれぞれの面積を考えると、 $1$ 辺の長さが $2 \rm cm2×2(2\textcolor{blue}空間図形の表面積比と体積比 右の図のように、2つの立体が相似ならば、対応する表面の図形も互いに相似である。 それゆえ、相似比が m n の図形の表面比は S S ′ = m 2 n 2 となる。 また、左の三角推の底面積と高さを T 、 h とすると、右の三角錐の底




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ



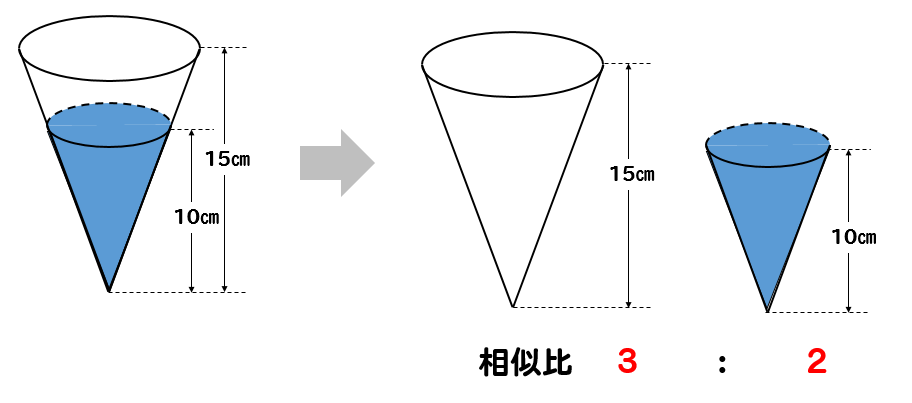
Studydoctor相似比と体積比 円錐台 中学3年数学 Studydoctor
相似な図形の体積比の問題です。基本を確認して、いろいろな応用問題を解けるようにしてください。基本事項相似比が a b である図形の面積の比は, a3 b3である。*簡単な証明もできるようにしましょう。例)1辺の長さaとbの立方体の場合相似比 → ab 体積は a3 と b3 よって上の基相似な図形の場合、 相似比を2乗して面積比を作りましょう! 面積比が分かったら、あとは楽勝だね (^^) 図形Bの面積を とおいて、比例式を作っていきましょう。 よって、図形Bの面積は ㎠ となります。 相似比の2乗だ! ってことを覚えておけば簡単です 相似な図形の面積比の問題です。基本を確認して、いろいろな応用問題を解けるようにしてください。基本事項相似比が m n である図形の面積の比は,m2 n2 である。例)下のような相似な三角形がある ABCと A'B'C'の相似比は 1:2面積を求めると ABC=4 A'B'C'=16 面積比は1:4相似比が1:2のとき



初中数学中关于位似中点问题的例题 初中数学位似题目




相似比と体積比 無料で使える中学学習プリント
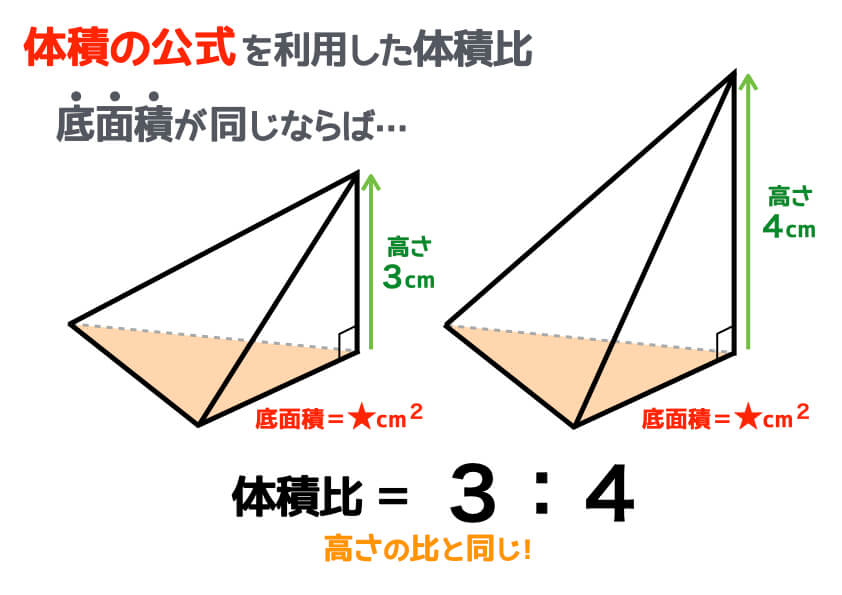
相似な立体の体積比 解説 平面図形と同じように立体図形においても,1つの立体を形を変えずに一定の割合で拡大または縮小して得られる立体は,もとの立体と 相似 であるといい,もとの立体との対応する部分の長さの比を 相似比 といいます。 体積比を用いた方が、簡単に問題を解くことが出来ることもありますので、基本事項をしっかり確認してください。 体積比の基本 相似比が a b のとき、体積比は (a×a×a) (b×b×b) となります。 ★ 1辺が1cmの立方体と1辺が2cmの立方体では 円すいと体積比 体積比が相似比の3乗になることは,面積比と同じような説明で納得できます。 体積比が3乗になることの大雑把な説明 直方体の場合について正しい(体積は縦×横×高さなので k k k 倍に拡大すると体積は k 3 k^3 k 3 倍になる)




中3 三角形の相似 円錐の体積比 日本語版 Youtube




比表面積計算shimadzu Ysctow




表面積體積比 Mojodor



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ




試辦會考數學 102 單選21 相似三角形面積比與柱體的體積 評量專區 均一教育平台
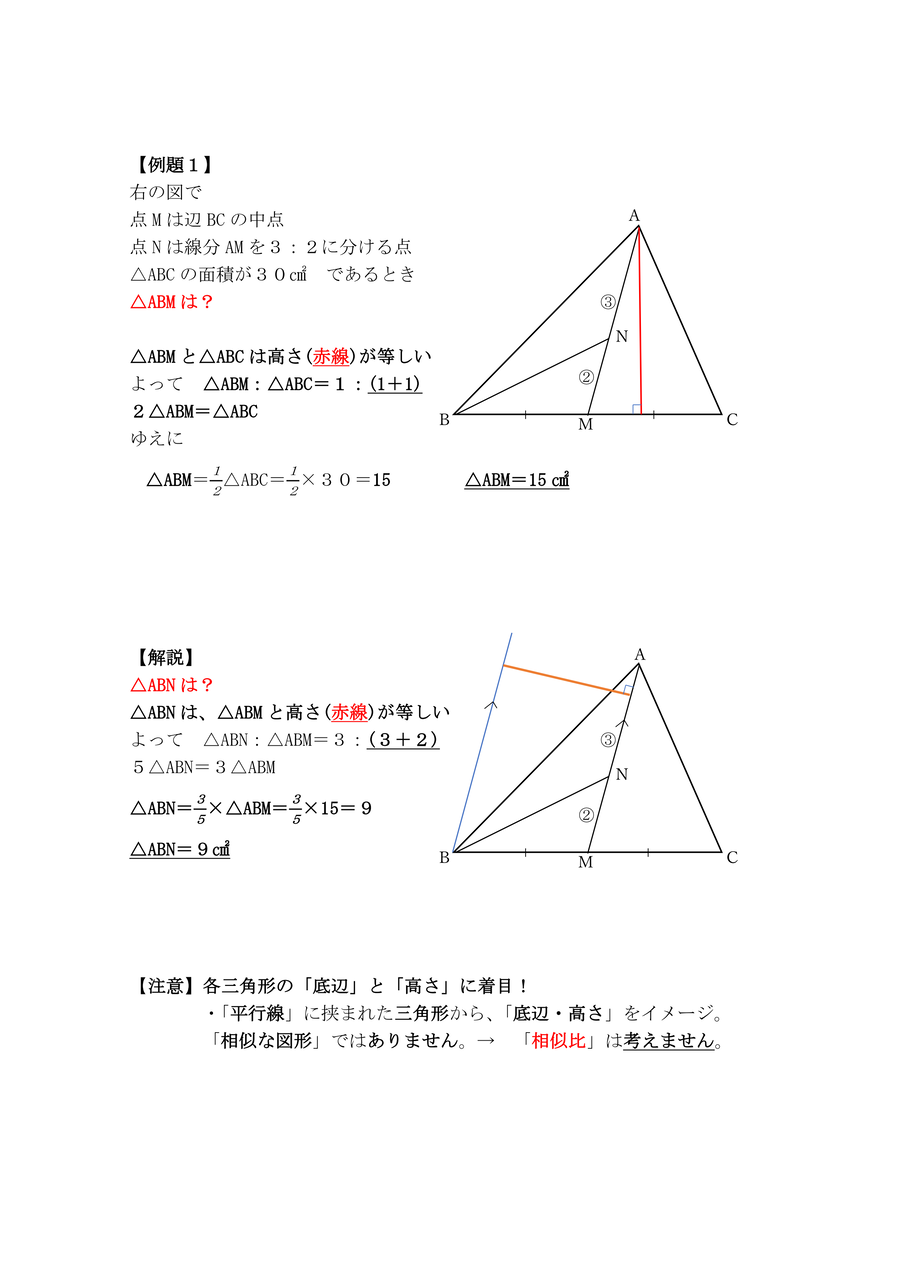



中学校数学 証明のコツ 面積比 体積比




高校入試 英語 数学 図形と相似 面積比と体積比



Studydoctor相似比と体積の計算 円錐台 三角錐台 中学3年数学 Studydoctor
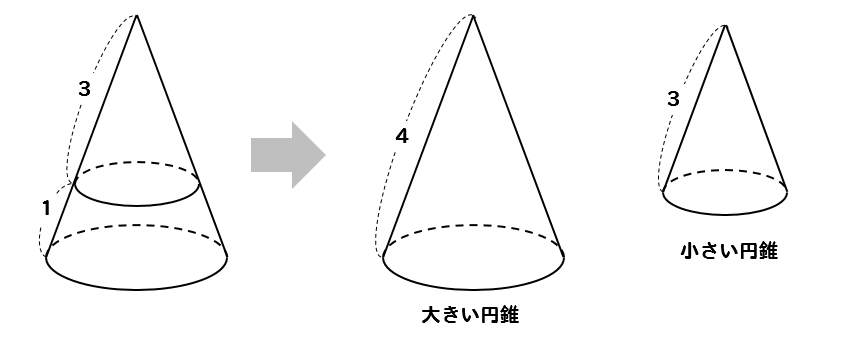



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ
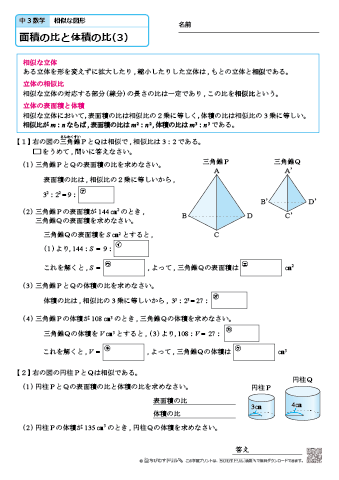



中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



2つの球の半径がそれぞれ5cm 2cmのとき相似比表面積比体積 Yahoo 知恵袋




比表面積公式比表面積 360百科 Utvos




比表面積公式比表面積 360百科 Utvos




数学 中3 54 相似と体積 基本編 Youtube




面积比是相似比的平方体积比是相似比的立方的详细说明是什么 百度知道




比表面積公式比表面積 360百科 Utvos
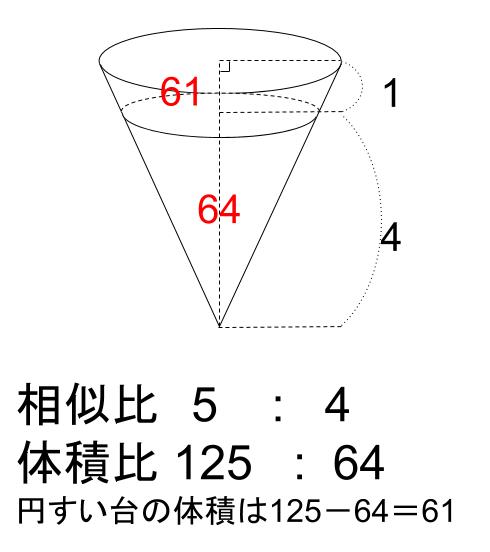



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su
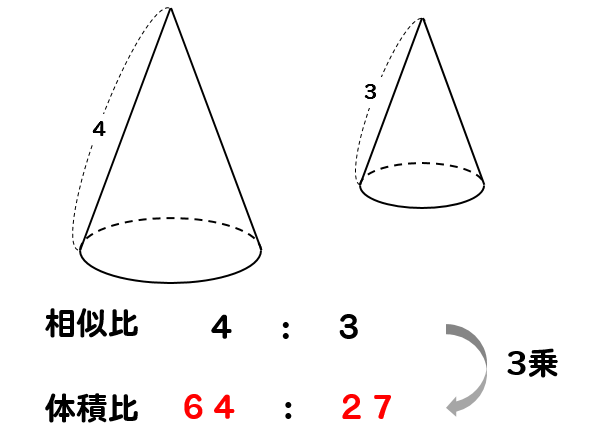



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



1



中三です 今日の数学で 円錐の相似比 体積比などを教わりました Yahoo 知恵袋
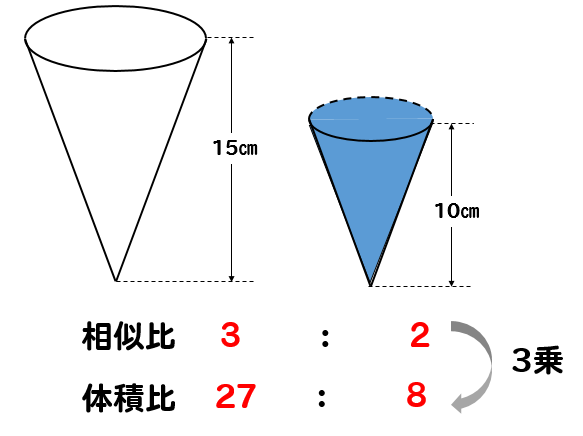



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ



1




相似な図形の面積と体積 の勉強法のわからないを5分で解決 映像授業のtry It トライイット




中学校数学 証明のコツ 面積比 体積比
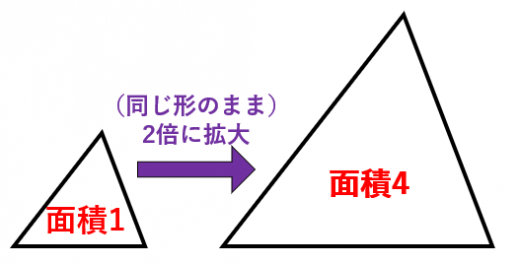



相似比と面積比 体積比の公式の証明 高校数学の美しい物語




表面積體積比 Mojodor




相似比と体積比 円錐台 中学3年数学 Youtube




相似比と体積比 無料で使える中学学習プリント
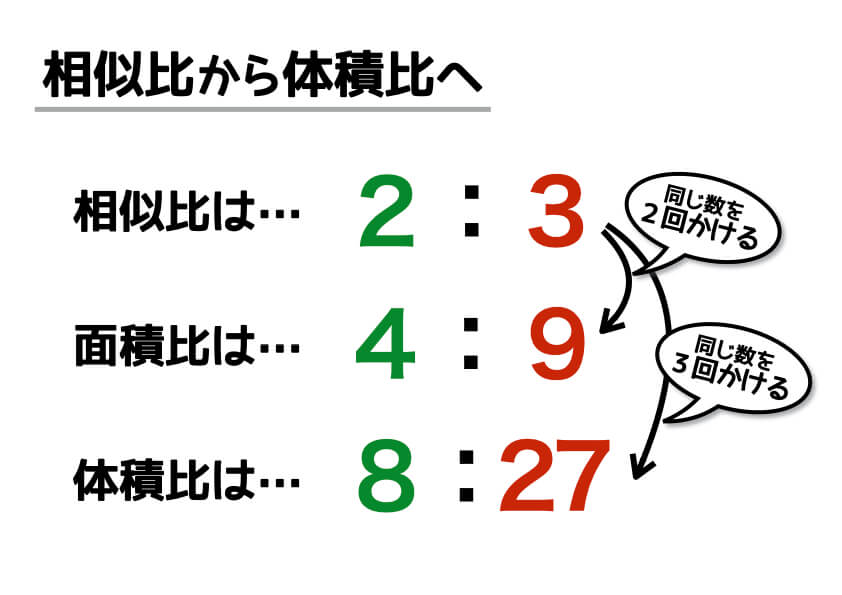



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ



中学3年の相似な立体の表面積の比と体積比の問題なんですけだ この写真の Yahoo 知恵袋




中3 数学 相似15 表面積比 体積比 9分 Youtube



1




図形の面積比 体積比 数学i フリー教材開発コミュニティ Ftext



受動態 相似比 面積比 体積比 今日の板書
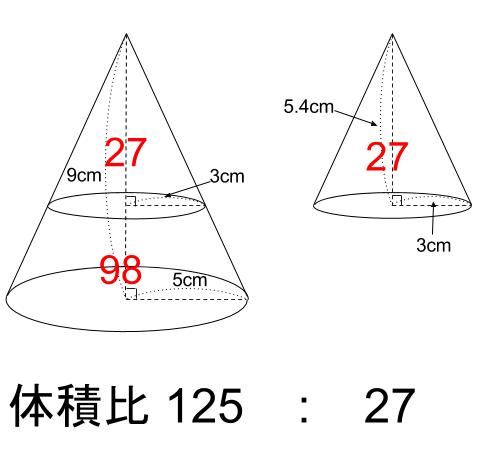



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su




相似な円柱の表面積比 体積比 中学数学 By Okボーイ マナペディア



第5章 面積の比と体積の比 台形の相似比と面積比




面積比と体積比 教遊者




相似比 面積比 体積比 一新ゼミ 金沢市にある小学生 中学生 高校生対象の塾




2つの相似な三角錐aとbがあって 相似比は2 3である Bの体積が135 Clearnote




比表面積計算shimadzu Ysctow



受動態 相似比 面積比 体積比 今日の板書
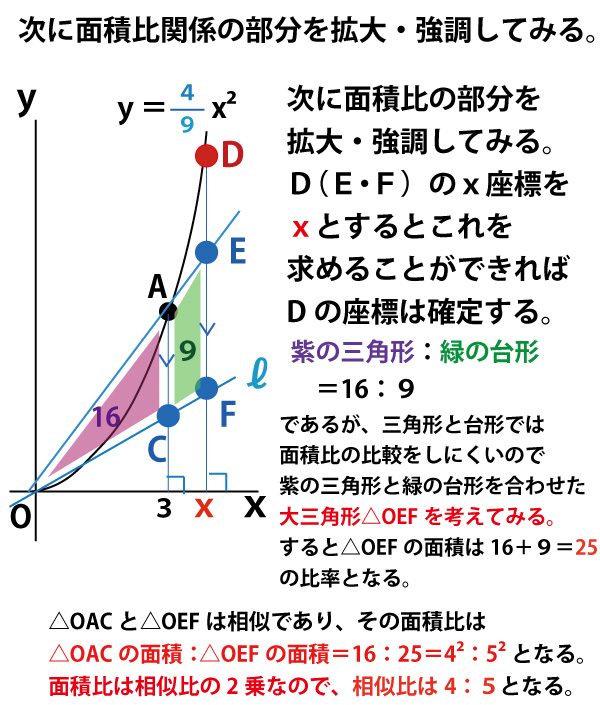



年前期 千葉県公立高校入試 数学 第3問 二次関数 問題 配点15点 解答 解説 動画 文字両方あり 船橋市議会議員 朝倉幹晴公式サイト




相似な直方体の表面積比 体積比 中学数学 By Okボーイ マナペディア



Studydoctor予習 テスト勉強前に 10分で丸わかり相似比と面積比 体積比まとめ 中学3年数学 Studydoctor



直观图与原图面积比 第1页 要无忧健康图库
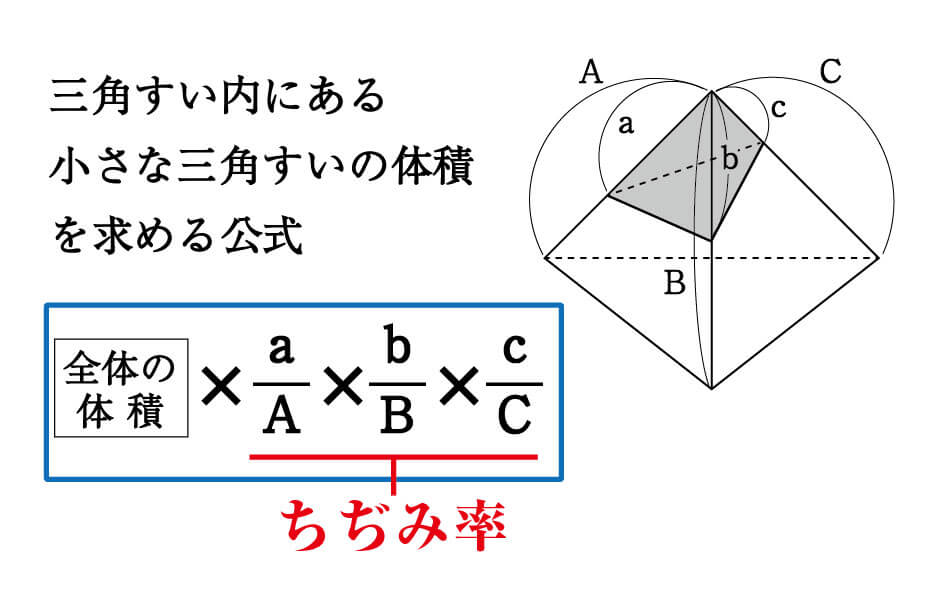



数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



中学3年数学練習問題 相似な立体の表面積と体積の比 図形と相似




中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su




比表面積公式比表面積 360百科 Utvos



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ




相似比と面積比 体積比の公式の証明 高校数学の美しい物語



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ



تويتر ここなん先生 あなたのおしりを軽くする على تويتر 相似な図形の面積比 体積比 相似比 長さの比 A B 面積比 A B 底面積比 表面積比でも 体積比a B 相似な図形のときしか使えないことに注意 T Co 2aieisbrjd




3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく



Math 相似比 面積比 体積比 面積比が2乗 体積比が3乗になる証明 働きアリ



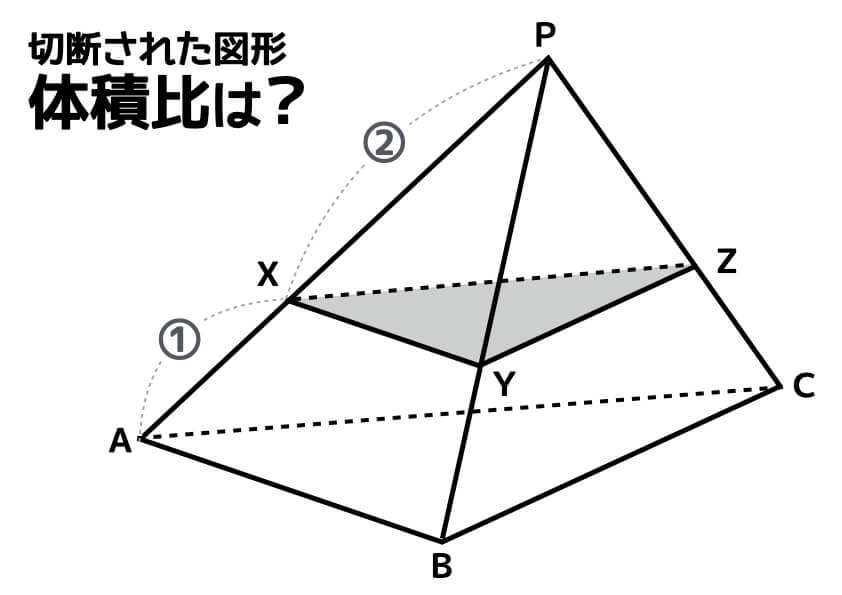
Math 空間図形と相似 面積比 体積比 発展問題 働きアリ



相似三角形的面積比與邊長對應關係比 Live 多媒體數學觀念典online



Math 相似比 面積比 体積比 面積比が2乗 体積比が3乗になる証明 働きアリ




立方定律 兩個幾何形狀相似物體對應長度比為a B 則對應體積比為a 3 百科知識中文網



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ
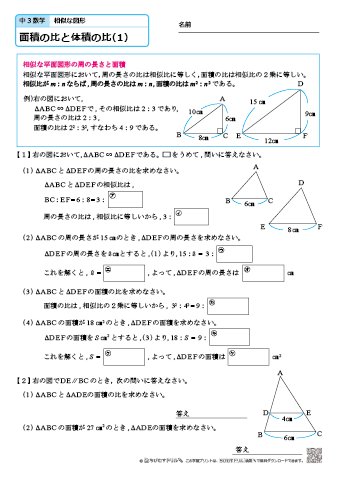



中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
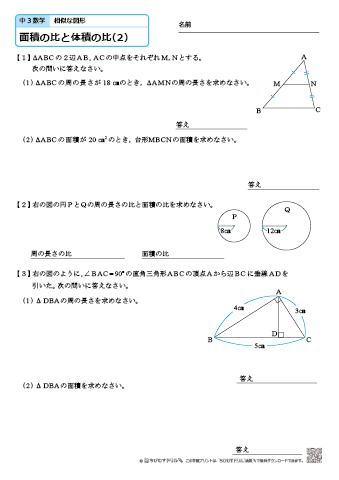



中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3数学 相似な図形の表面積比 体積比 映像授業のtry It トライイット



1



相似三角形的性质 相似ppt 第一ppt
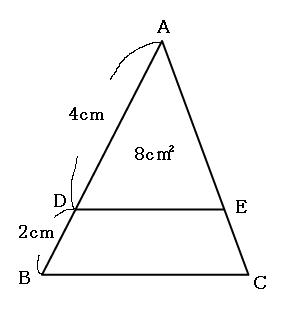



相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう




比表面積公式比表面積 360百科 Utvos




中三 面積和體積 相似形狀對應邊的比與體積的比之關係 Youtube




比例的應用長度比面積比及體積比的關係 Youtube
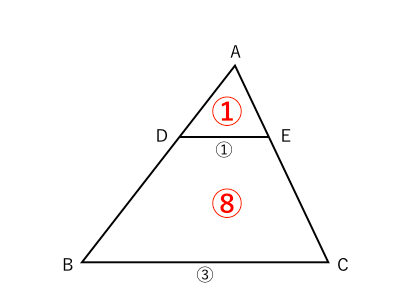



相似比と面積比と体積比はお友だち 苦手な数学を簡単に




比例的應用長度比面積比及體積比的關係 Youtube
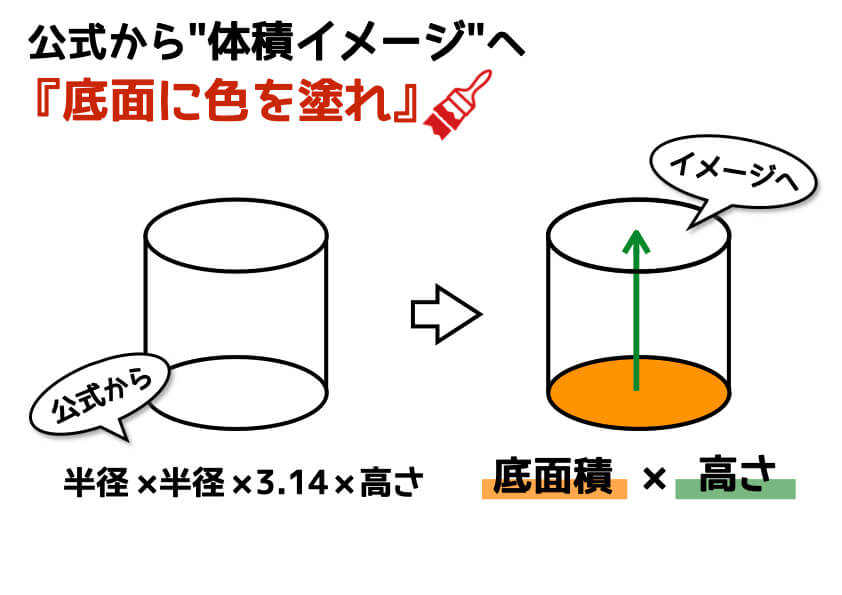



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ




相似比と体積比 無料で使える中学学習プリント
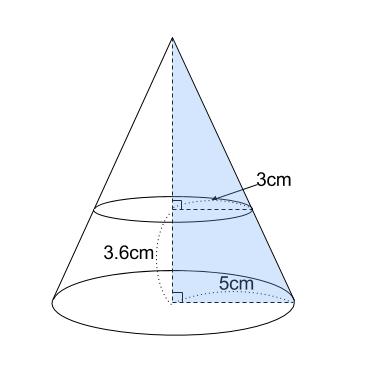



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su




覚えて損はない 相似な立体同士の3つの性質 Qikeru 学びを楽しくわかりやすく




圆锥侧面积公式推导图 巧记空间几何体的面积和体积公式 破锁网
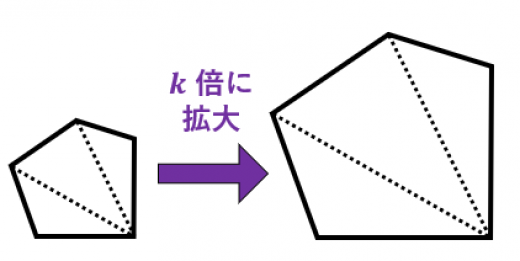



相似比と面積比 体積比の公式の証明 高校数学の美しい物語



この正四角錐のpとaの体積比の求め方が分かりません 答えは27 19です Yahoo 知恵袋
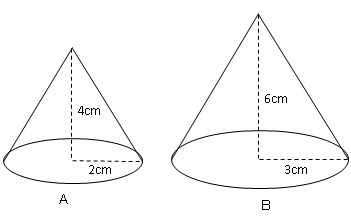



相似と体積比 1 ネット塾




相似比と体積比 無料で使える中学学習プリント




相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう
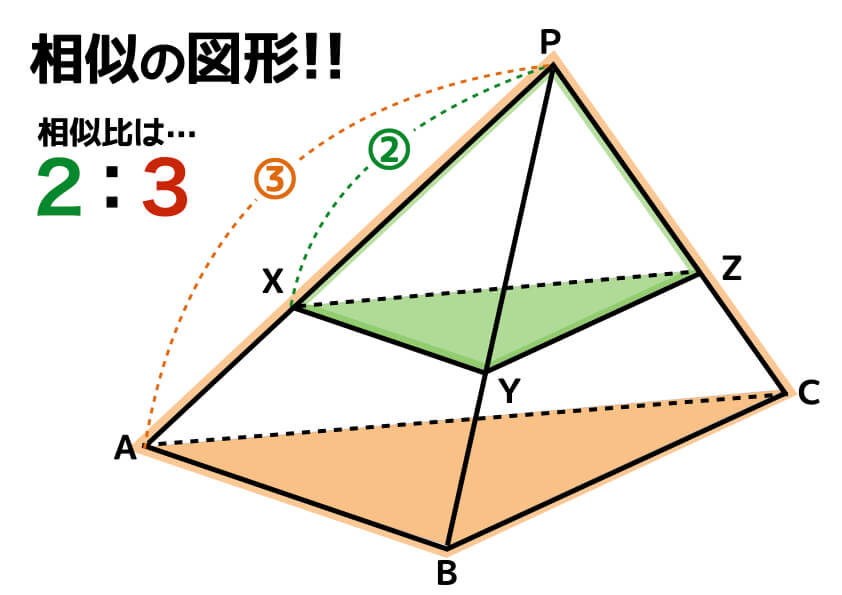



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ




面積比と体積比 教遊者




比表面積計算shimadzu Ysctow
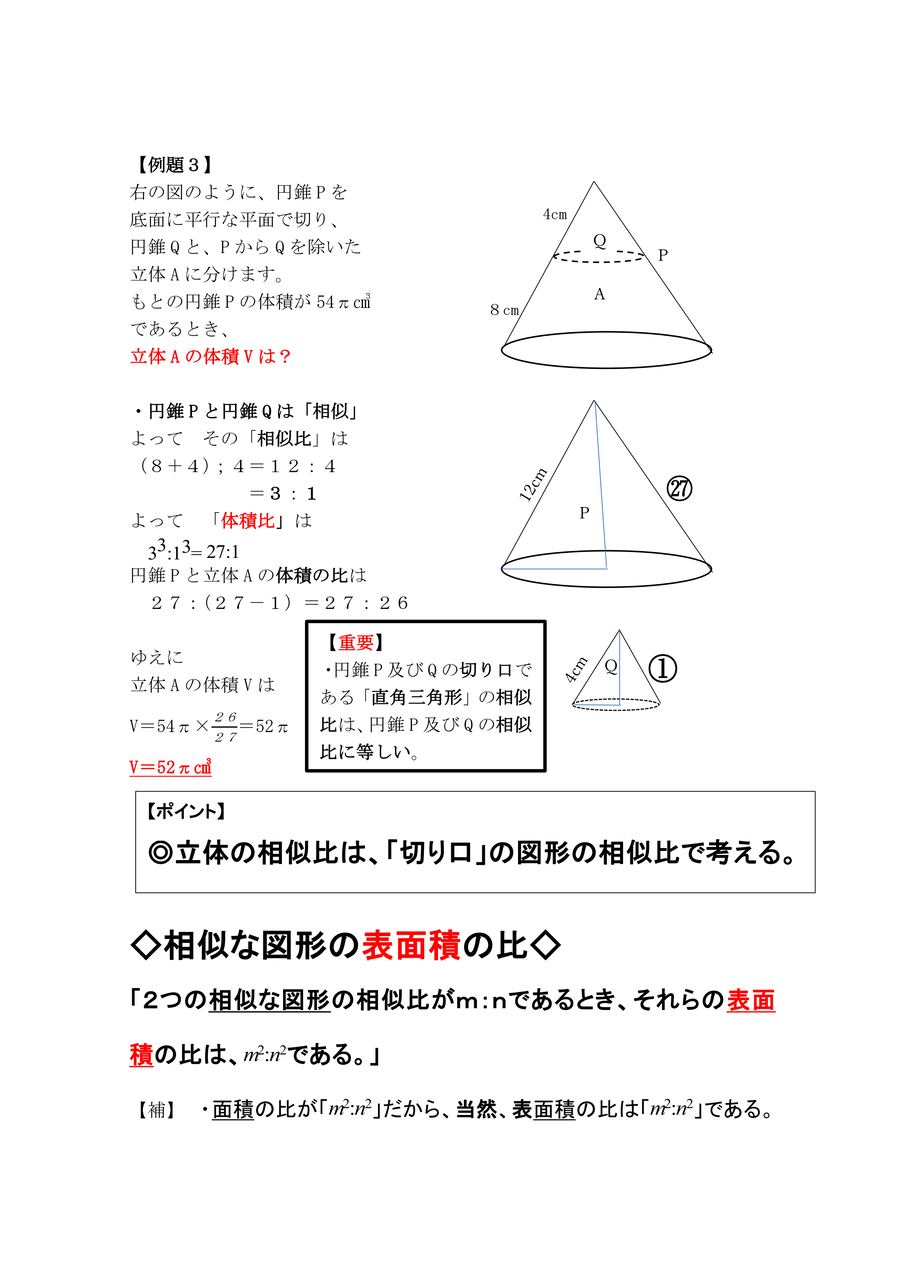



中学校数学 証明のコツ 面積比 体積比




3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく
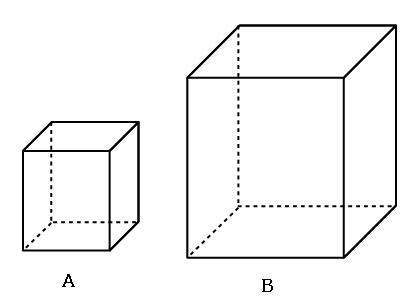



相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう




Ratio Of Areas And Volumes Of Similar Figures 相似圖形的面積比和體積比 Geogebra




中3数学 相似な図形の表面積比 体積比 練習編 映像授業のtry It トライイット




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




比表面積公式比表面積 360百科 Utvos



立体の相似と表面積比 体積比 チーム エン
コメント
コメントを投稿